Angle Sum Property Of A Triangle

Theorem: Sum of the interior angles of a triangle is $180^o$.

Prerequisites:
Alternate angles property (proof)
Angle on a straight line property (proof)

Proof:

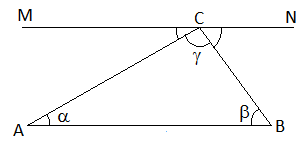
In the given figure, let ABC be any triangle with interior angles $= \alpha, \beta \text{ and } \gamma$, at the vertices A, B and C respectively.

Now draw a line MN through the point C, such that MN$\parallel$AB.

Therefore, by alternate angles property,

$\qquad\quad\angle MCA = \angle A = \alpha$
And, $\;\;\angle NCB = \angle B = \beta$

Since, MN is a straight line,

hence, $\;\angle MCA + \angle NCB + \angle ACB = 180^o$
$\Rightarrow\quad\;\;\alpha + \beta + \gamma = 180^o$

Hence the result.


Recommended:
Angle Sum Property of polygon
Isosceles Triangle Theorem
AAA similarity